python回归分析逻辑斯蒂模型之多分类任务详解 目录 逻辑斯蒂回归模型多分类任务 1.ovr策略 2.one vs one策略 3.softmax策略 逻辑斯蒂回归模型多分类案例实现 逻辑斯蒂回归模型多分类任务 上节中,我们使用逻辑斯蒂回归完成了二分类任务,针对多分类任
目录
- 逻辑斯蒂回归模型多分类任务
- 1.ovr策略
- 2.one vs one策略
- 3.softmax策略
- 逻辑斯蒂回归模型多分类案例实现
逻辑斯蒂回归模型多分类任务
上节中,我们使用逻辑斯蒂回归完成了二分类任务,针对多分类任务,我们可以采用以下措施,进行分类。
我们以三分类任务为例,类别分别为a,b,c。
1.ovr策略
我们可以训练a类别,非a类别的分类器,确认未来的样本是否为a类; 同理,可以训练b类别,非b类别的分类器,确认未来的样本是否为b类; 同理,可以训练c类别,非c类别的分类器,确认未来的样本是否为c类;这样我们通过增加分类器的数量,K类训练K个分类器,完成多分类任务。
2.one vs one策略
我们将样本根据类别进行划分,分别训练a与b、a与c、b与c之间的分类器,通过多个分类器判断结果的汇总打分,判断未来样本的类别。 同样使用了增加分类的数量的方法,需要注意训练样本的使用方法不同,K类训练K(K-1)/2个分类器,完成多分类任务
3.softmax策略
通过计算各个类别的概率,比较最高概率后,确定最终的类别。
对于类别互斥的情况,建议使用softmax,而不同类别之间关联性较强时,建议使用增加多个分类器的策略。
逻辑斯蒂回归模型多分类案例实现
本例我们使用sklearn数据集,鸢尾花数据。
1.加载数据
- 样本总量:150组
- 预测类别:山鸢尾,杂色鸢尾,弗吉尼亚鸢尾三类,各50组。
- 样本特征4种:花萼长度sepal length (cm) 、花萼宽度sepal width (cm)、花瓣长度petal length (cm)、花瓣宽度petal width (cm)。
2.使用seaborn提供的pairplot方法,可视化展示特征与标签
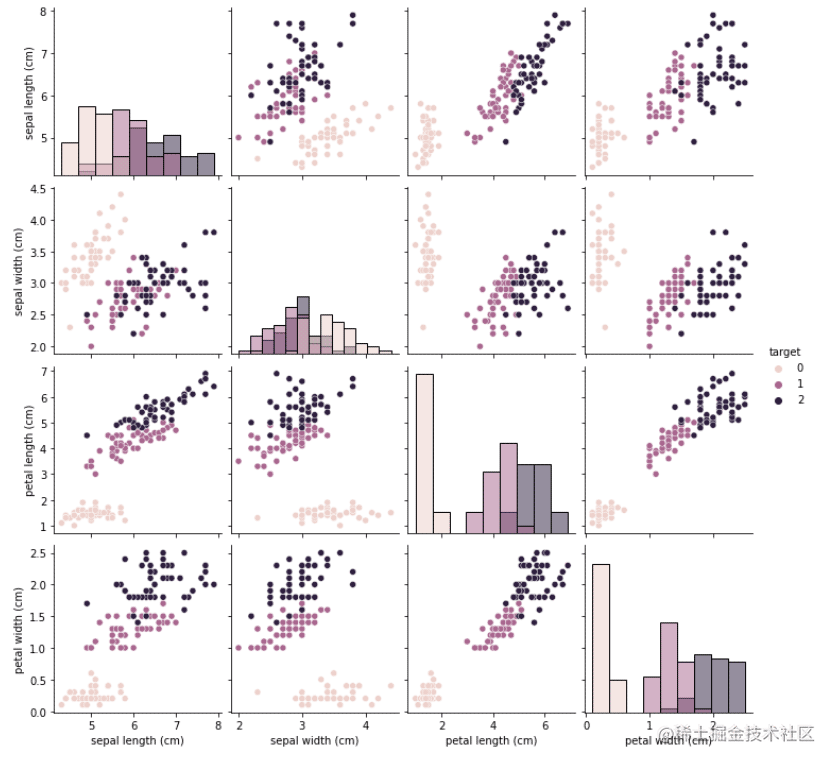
3.训练模型
from sklearn.datasets import load_iris
import pandas as pd
import seaborn as sns
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split
#加载数据
data = load_iris()
iris_target = data.target #
iris_df = pd.DataFrame(data=data.data, columns=data.feature_names) #利用Pandas转化为DataFrame格式
iris_df['target'] = iris_target
## 特征与标签组合的散点可视化
sns.pairplot(data=iris_df,diag_kind='hist', hue= 'target')
plt.show()
#划分数据集
X=iris_df.iloc[:,:-1]
y=iris_df.iloc[:,-1]
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
## 创建逻辑回归模型
clf = LogisticRegression(random_state=0, solver='lbfgs')
''' 优化算法选择参数:solver\
solver参数决定了我们对逻辑回归损失函数的优化方法,有4种算法可以选择,分别是:
a) liblinear:使用了开源的liblinear库实现,内部使用了坐标轴下降法来迭代优化损失函数。
b) lbfgs:拟牛顿法的一种,利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
c) newton-cg:也是牛顿法家族的一种,利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
d) sag:即随机平均梯度下降,是梯度下降法的变种,和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度,适合于样本数据多的时候。
从上面的描述可以看出,newton-cg, lbfgs和sag这三种优化算法时都需要损失函数的一阶或者二阶连续导数,因此不能用于没有连续导数的L1正则化,只能用于L2正则化。而liblinear通吃L1正则化和L2正则化。
同时,sag每次仅仅使用了部分样本进行梯度迭代,所以当样本量少的时候不要选择它,而如果样本量非常大,比如大于10万,sag是第一选择。但是sag不能用于L1正则化,所以当你有大量的样本,又需要L1正则化的话就要自己做取舍了。要么通过对样本采样来降低样本量,要么回到L2正则化。
从上面的描述,大家可能觉得,既然newton-cg, lbfgs和sag这么多限制,如果不是大样本,我们选择liblinear不就行了嘛!错,因为liblinear也有自己的弱点!我们知道,逻辑回归有二元逻辑回归和多元逻辑回归。对于多元逻辑回归常见的有one-vs-rest(OvR)和many-vs-many(MvM)两种。而MvM一般比OvR分类相对准确一些。郁闷的是liblinear只支持OvR,不支持MvM,这样如果我们需要相对精确的多元逻辑回归时,就不能选择liblinear了。也意味着如果我们需要相对精确的多元逻辑回归不能使用L1正则化了。
'''
clf.fit(x_train, y_train)
## 查看自变量对应的系数w
print('the weight of Logistic Regression:\n',clf.coef_)
## 查看常数项对应的系数w0
print('the intercept(w0) of Logistic Regression:\n',clf.intercept_)
#模型1的变量重要性排序
coef_c1 = pd.DataFrame({'var' : pd.Series(x_test.columns),
'coef_abs' : abs(pd.Series(clf.coef_[0].flatten()))
})
coef_c1 = coef_c1.sort_values(by = 'coef_abs',ascending=False)
print(coef_c1)
#模型2的变量重要性排序
coef_c2 = pd.DataFrame({'var' : pd.Series(x_test.columns),
'coef_abs' : abs(pd.Series(clf.coef_[1].flatten()))
})
coef_c2 = coef_c2.sort_values(by = 'coef_abs',ascending=False)
print(coef_c2)
#模型3的变量重要性排序
coef_c3 = pd.DataFrame({'var' : pd.Series(x_test.columns),
'coef_abs' : abs(pd.Series(clf.coef_[2].flatten()))
})
coef_c3 = coef_c3.sort_values(by = 'coef_abs',ascending=False)
print(coef_c3)
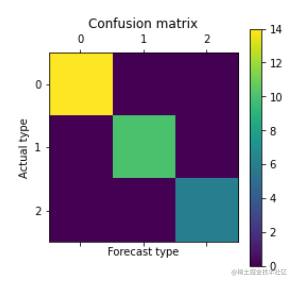
4.对模型进行评价:模型得分、交叉验证得分、混淆矩阵
from sklearn.metrics import accuracy_score,recall_score
## 模型评价
score = clf.score(x_train,y_train)#Return the mean accuracy on the given test data and labels.
print(score)#0.628125
#模型在训练集上的得分
train_score = accuracy_score(y_train,clf.predict(x_train))
print(train_score)#0.628125
#模型在测试集上的得分
test_score = clf.score(x_test,y_test)
print(test_score)#0.6
#预测
y_predict = clf.predict(x_test)
#训练集的召回率
train_recall = recall_score(y_train, clf.predict(x_train), average='macro')
print("训练集召回率",train_recall)#0.47934382086167804
#测试集的召回率
test_recall = recall_score(y_test, clf.predict(x_test), average='macro')
print("测试集召回率",test_recall)#0.5002736726874658
from sklearn.metrics import classification_report
print('测试数据指标:\n',classification_report(y_test,y_predict,digits=4))
#k-fold交叉验证得分
from sklearn.model_selection import cross_val_score
scores = cross_val_score(clf,x_train,y_train,cv=10,scoring='accuracy')
print('十折交叉验证:每一次的得分',scores)
#结果:每一次的得分 [0.59375 0.59375 0.6875 0.59375 0.53125 0.5625 0.65625 0.625 0.71875 0.625 ]
print('十折交叉验证:平均得分', scores.mean())
#结果:平均得分 0.61875
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import confusion_matrix
import pandas as pd
labelEncoder = LabelEncoder()
labelEncoder.fit(y)##对变量y进行硬编码,将标签变为数字
cm = confusion_matrix(y_test, y_predict)
cm_pd = pd.DataFrame(data = cm,columns=labelEncoder.classes_, index=labelEncoder.classes_)
print("混淆矩阵")
print(cm_pd)
import matplotlib.pyplot as plt
plt.matshow(confusion_matrix(y_test, y_predict))
plt.title('Confusion matrix')
plt.colorbar()
plt.ylabel('Actual type') #实际类型
plt.xlabel('Forecast type') #预测类型
以上就是python回归分析逻辑斯蒂模型之多分类任务详解的详细内容,更多关于python逻辑斯蒂模型的资料请关注我们其它相关文章!
本文标题为:python回归分析逻辑斯蒂模型之多分类任务详解


- python中列表添加元素的几种方式(+、append()、ext 2022-09-02
- python中defaultdict用法实例详解 2022-10-20
- Python实现将DNA序列存储为tfr文件并读取流程介绍 2022-10-20
- Python 保存数据的方法(4种方法) 2023-09-04
- windows安装python2.7.12和pycharm2018教程 2023-09-03
- 在centos6.4下安装python3.5 2023-09-04
- Python之路-Python中的线程与进程 2023-09-04
- CentOS7 安装 Python3.6 2023-09-04
- Python Pandas如何获取和修改任意位置的值(at,iat,loc,iloc) 2023-08-04
- python线程池ThreadPoolExecutor与进程池ProcessPoolExecutor 2023-09-04