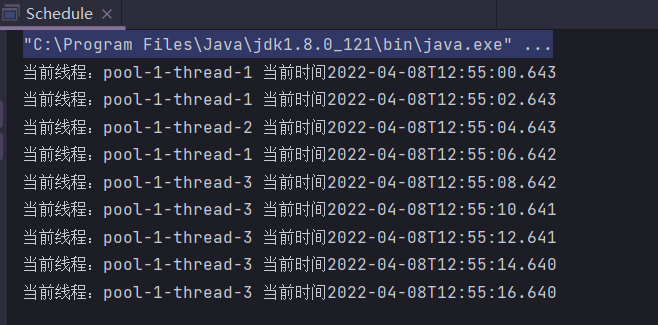
在Java中,我们使用二维数组的实现方式,将每一个值赋予其对应的杨辉三角位置,从而形成了整个杨辉三角的形结构。
一、算法概述
杨辉三角,又称Pascal三角形,其性质有:第n行的数字个数等于n,第n行的m个数可以表示为C(n-1,m-1),也可以理解为每个数字A[i][j]可以由它的左上方的数字A[i-1][j-1]和上方的数字A[i-1][j]相加的结果。
int[][] triangle = new int[numRows][];
for (int i = 0; i < numRows; i++) {
triangle[i] = new int[i + 1];
triangle[i][0] = 1;
triangle[i][i] = 1;
for (int j = 1; j < i; j++) {
triangle[i][j] = triangle[i - 1][j - 1] + triangle[i - 1][j];
}
}
以上代码依次定义了杨辉三角,并进行了赋值,只留下每一行最后一个数字待求解。
二、杨辉三角性质和Java实现
在Java中,每行的数据是根据上一行的数据计算得出。例如第二行的数据就是第一行数据两边各加了一个0得到的,第三行就是第二行数据两边再各加一个0得到的,以此类推。
for (int i = 0; i < numRows; i++) {
for (int j = 1; j < i; j++) {
triangle[i][j] = triangle[i - 1][j - 1] + triangle[i - 1][j];
}
}
以上代码利用二重循环计算出每一行最后一个数字的位置,并完成赋值。
三、打印杨辉三角
计算结果后,我们将杨辉三角进行打印,由于杨辉三角是个等腰三角形,所以在打印时需要前面需要打印空格,数量等于总行数减去当前行数。
for (int i = 0; i < numRows; i++) {
for (int j = 0; j < numRows - i; j++) {
System.out.print(" ");
}
for (int k = 0; k <= i; k++) {
System.out.print(triangle[i][k] + " ");
}
System.out.println();
}
以上代码实现了杨辉三角的等腰排列,有助于我们对其内在规律的理解。
沃梦达教程
本文标题为:Java实现杨辉三角


猜你喜欢
- ExecutorService Callable Future多线程返回结果原理解析 2023-06-01
- Springboot整合minio实现文件服务的教程详解 2022-12-03
- JSP 制作验证码的实例详解 2023-07-30
- SpringBoot使用thymeleaf实现一个前端表格方法详解 2023-06-06
- Java实现顺序表的操作详解 2023-05-19
- Java中的日期时间处理及格式化处理 2023-04-18
- 深入了解Spring的事务传播机制 2023-06-02
- JSP页面间传值问题实例简析 2023-08-03
- 基于Java Agent的premain方式实现方法耗时监控问题 2023-06-17
- Spring Security权限想要细化到按钮实现示例 2023-03-07